Was ist der K-Faktor einer Abkantpresse und wie berechnet man ihn?

Was ist der K-Faktor einer Abkantpresse?

Der Abkantpresse Der K-Faktor, auch Biegetoleranzfaktor genannt, ist ein dimensionsloser Parameter, der beim Biegen von Blechen verwendet wird, um die während des Biegevorgangs auftretende Materialdehnung zu bestimmen. Er hilft bei der Berechnung der Biegetoleranz, also der zusätzlichen Materiallänge, die zum Biegen erforderlich ist.

Der K-Faktor berücksichtigt die Materialdicke, den Biegeradius und die Eigenschaften des zu biegenden Materials. Er stellt im Wesentlichen das Verhältnis zwischen dem Abstand vom Innenradius der Biegung zur neutralen Achse des Materials und der Materialdicke dar.

Ein niedrigerer K-Faktor bedeutet eine geringere Materialdehnung beim Biegen, während ein höherer K-Faktor eine stärkere Dehnung anzeigt. Der K-Faktor ist entscheidend für die genaue Vorhersage des endgültigen Biegewinkels und das Erreichen präziser Biegemaße bei der Blechbearbeitung.

Um den richtigen K-Faktor für ein bestimmtes Material und eine bestimmte Biegekonfiguration zu ermitteln, sind häufig Experimente oder das Nachschlagen in Materialangaben erforderlich. Er kann je nach Faktoren wie Materialtyp, Dicke, Werkzeug und Biegemethode variieren. Nach der Ermittlung wird der K-Faktor normalerweise in Biegezugabeformeln verwendet, um die Materialdehnung zu berechnen und genaue Biegemaße zu erzielen.

Biegen eines Probestücks

Reverse Engineering des K-Faktors für Abkantpresse ist die einzige Möglichkeit, den tatsächlichen Wert zu bestimmen, oder zumindest einen, der so nah wie möglich am perfekten Wert liegt. Sie können dies tun, indem Sie Testbiegungen durchführen, die Ergebnisse messen und den K-Faktor aus der BA-Formel extrahieren, die die von Ihnen gemessenen Ergebnisse enthält. Dies könnte Ihre beste Option sein, insbesondere wenn Sie eine Tabelle erstellen.

Aber – und das ist ein großes Aber – Sie müssen auch die Materialtoleranzen berücksichtigen, einschließlich Zugfestigkeit, Streckgrenze und Dicke. Sie könnten einige sehr genaue K-Faktor-Daten von einem Teststück erhalten, aber das Material des Teststücks entspricht möglicherweise nicht den Eigenschaften des Materials, das Sie in der Produktion biegen. Unabhängig davon, ob Sie den BA gerade durch Biegen von Teststücken ermittelt haben, benötigen Sie den K-Faktor möglicherweise ohnehin nicht.

Berechnung des K-Faktors, kein Teststück erforderlich

Es gibt eine andere Möglichkeit, den K-Faktor zu berechnen, ohne Teststücke zu biegen. Diese Methode ist nicht perfekt, aber das Biegen eines Teststücks ist es auch nicht. Nicht nur die Materialeigenschaften können sich ändern, sondern auch die genauen Eigenschaften der verwendeten Werkzeuge (unterschiedliche Reibungsgrade) und verschiedene Formgebungsmethoden.

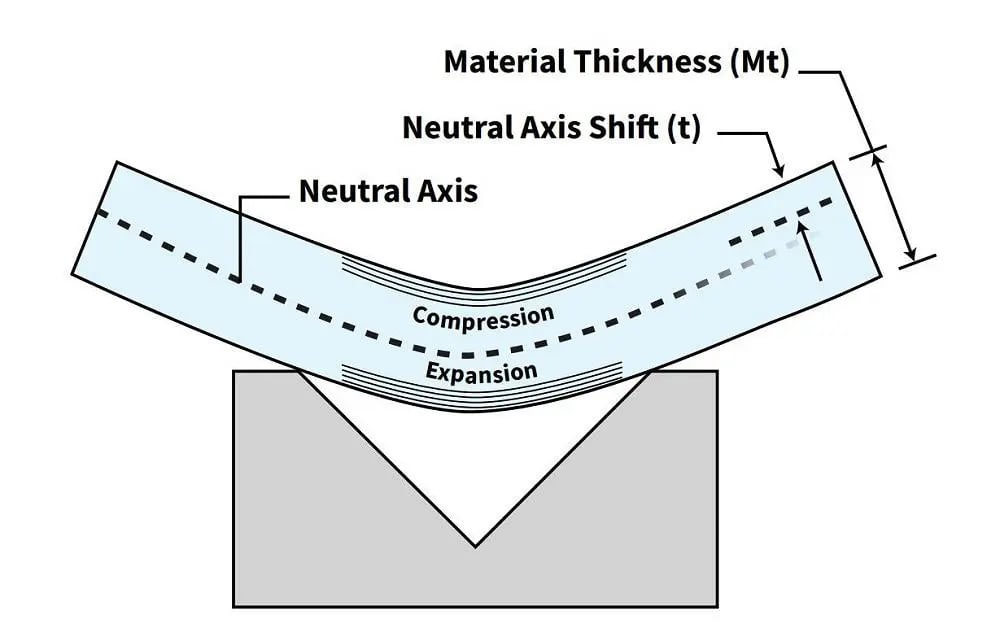
Abbildung zeigt den K-Faktor beim Blechbiegen

ABBILDUNG 1. Der K-Faktor, ausgedrückt als t/Mt, ist ein Verhältnis, das die Verschiebung der neutralen Achse nach innen während der Biegung beschreibt.

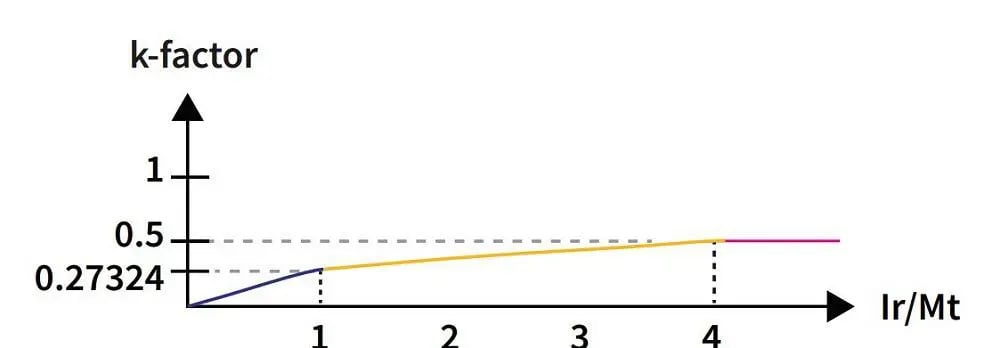
Nach alledem können Sie mit der grafischen Darstellung des K-Faktors beginnen, wie in Abbildung 3 dargestellt. Diese zeigt den Maximalwert für den K-Faktor bei 50% der Materialstärke, gekennzeichnet durch die rote Linie. Wo sich die gelbe und die rote Linie treffen (Punkt 4 im Diagramm), entspricht dies einem inneren Biegeradius, der dem Vierfachen der Materialstärke entspricht. Darüber hinaus berechnen Sie Faktoren, die größer als 50% sind, aber Sie sollten diese nicht verwenden. Wie das Diagramm zeigt, müssen Sie Ihren K-Faktor bei diesem Maximalwert von 0,50 halten.

Position 1 im Diagramm, wo die blaue und die gelbe Linie zusammentreffen, ist der K-Faktor-Wert für einen scharfen oder minimal erzeugbaren Innenradius für eine Luftform. Jeder Wert darunter bringt die Biegung in einen Bereich, der die physikalischen Grenzen der Kompressibilität überschreitet – zumindest für unser Basismaterial, Weichstahl. Wie ich schon oft gesagt habe, sind scharfe Biegungen der Fluch der Genauigkeit bei der Luftformung.

Der minimale K-Faktor für die Luftformung kann als (4-π)/π oder 0,27324 ausgedrückt werden. Wir ziehen diesen Wert von unserem maximalen K-Faktor-Wert von 0,5 ab:

0.5 – 0.27324 = 0.22676

Dieses Ergebnis gibt uns unseren Bereich möglicher K-Faktoren, wie auf der gelben Linie im Diagramm angegeben. Als nächstes teilen wir 0,22676 durch 3:

0.2267/3 = 0.07558

Dadurch erhalten wir unseren Multiplikator, also die Zahl, die wir mit dem Verhältnis von Innenradius zu Materialstärke unserer Biegung multiplizieren. Dieses Verhältnis ermitteln wir, indem wir den Innenradius der Biegung durch die Materialstärke dividieren. Ich verwende einen Innenradius von 0,093 Zoll bei 0,062 Zoll dickem Material.

0.093/0.062 = 1.5

Anschließend multiplizieren wir mit unserem Multiplikator 0,07558 und addieren das Ergebnis zum minimalen K-Faktor von 0,273:

0,07558 × 1,5 = 0,113

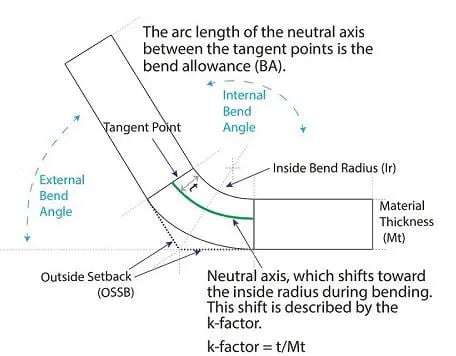
Abbildung, die den K-Faktor und den äußeren Rückschlag beim Biegen von Metall zeigt
ABBILDUNG 2. Der K-Faktor beschreibt die Verschiebung der neutralen Achse nach innen während des Biegens. Diese Verschiebung bewirkt eine Dehnung des Metalls, die wir in unseren Biegeberechnungen berücksichtigen.

0.113 + 0.273 = 0.386

Das ergibt einen K-Faktor von 0,386. All dies lässt sich in der folgenden Formel zusammenfassen. Auch hier leiten Sie den minimalen K-Faktor und Multiplikator aus dem Diagramm in Abbildung 2 ab.

K-Faktor = [Multiplikator × (Innenradius/Materialstärke)] + Minimaler K-Faktor

Aufschlüsselung der Biegezugabe

Sie haben den K-Faktor ermittelt. Und was nun? Was machen wir mit dieser Zahl? Wie wird sie angewendet und warum sollte sie Sie interessieren? Warum sie Sie interessieren sollte, hängt von der Qualität des Produkts ab, das Sie herstellen möchten. Das Verständnis des K-Faktors macht einen großen Unterschied. Sehen Sie sich zunächst Ihre BA-Formel an:

BA = [(0,017453 × Innenbiegeradius) + (0,0078 × Materialstärke)] × Außenbiegewinkel

In dieser Gleichung ist 0,017453 gleich π/180, wodurch Grad in Radiant oder Maßeinheiten für Winkel basierend auf dem Radius eines Kreises umgewandelt werden. Wir führen diese Umwandlung durch, weil trigonometrische Funktionen in mathematischen Berechnungen normalerweise Winkel in Radiant und nicht in Grad erfordern. Wenn Sie den umgewandelten Winkel (in Radiant) mit dem Radius multiplizieren, berechnen Sie im Wesentlichen die Länge entlang des Kreisbogens, der durch die Biegung gebildet wird. π/180 multipliziert mit dem Innenradius stellt also die Bogenlänge entlang der neutralen Achse für einen Winkelgrad dar.

Der zweite Teil der Gleichung beginnt wieder mit der Umrechnung von Grad in Radiant (π/180), die dann mit einem K-Faktor von 0,4468 multipliziert wird, wodurch wir die Zahl 0,0078 in der Formel erhalten. Dies stellt die Kompensation dar, die auftritt, wenn sich die neutrale Achse beim Biegen nach innen verschiebt, wodurch sich das Material dehnt und die Teileabmessungen verlängert werden.

Wir kennen jetzt die Gesamtlänge des Bogens und die zusätzliche Länge, die durch die Verschiebung der neutralen Achse entsteht. Bisher haben wir jedoch nur einen Biegewinkel von einem Grad berechnet. Jetzt multiplizieren wir den gesamten äußeren Biegewinkel, gemessen von der Außenseite der Biegung. (Hinweis: Verwenden Sie bei der Berechnung der BA niemals den inneren Biegewinkel.)

Ein Faktor unter vielen

Beachten Sie, dass viele Variablen Ihre K-Faktor-Werte durcheinanderbringen können, insbesondere wenn Bediener unterschiedliche Matrizenöffnungen wählen oder unterschiedliche Umformungsmethoden verwenden. Was ist also die „beste“ Möglichkeit, Ihre K-Faktor-Tabellen neu zu berechnen? Vielleicht ist es eine Excel-Tabelle. Vielleicht können Sie Teststücke biegen. Sie müssen nur wissen, dass der K-Faktor nur eine von vielen Variablen ist, die Sie berücksichtigen müssen.