Table des matières
Présentation de la cisaille à guillotine
Le cisaille à guillotine offre une efficacité, une précision et une fiabilité supérieures par rapport au cisaillement à poutre pivotante car il élimine le jeu dans la structure et permet d'ajuster l'angle de cisaillement.
Cependant, lors de la découpe de plaques larges et lourdes ou de plaques minces à haute résistance, la cisaille à guillotine peut être confrontée à des défis tels que la déformation de la machine affectant la précision de la coupe.
La plupart des recherches dans ce domaine se concentrent sur l’impact des paramètres de cisaillement sur la précision, la conception et l’automatisation du système de contrôle, ou la simulation du processus de cisaillement à l’aide de points discrets.
Cependant, il existe peu de recherches sur l’analyse des propriétés mécaniques et l’optimisation de la structure des cisaille à guillotine.
Cet article vise à combler cette lacune en analysant les caractéristiques statiques et dynamiques de la machine-outil et en simulant le processus de cisaillement des plaques. Grâce à cette analyse, des données de cisaillement continu sont obtenues et un schéma d'optimisation est proposé.
Analyse statique
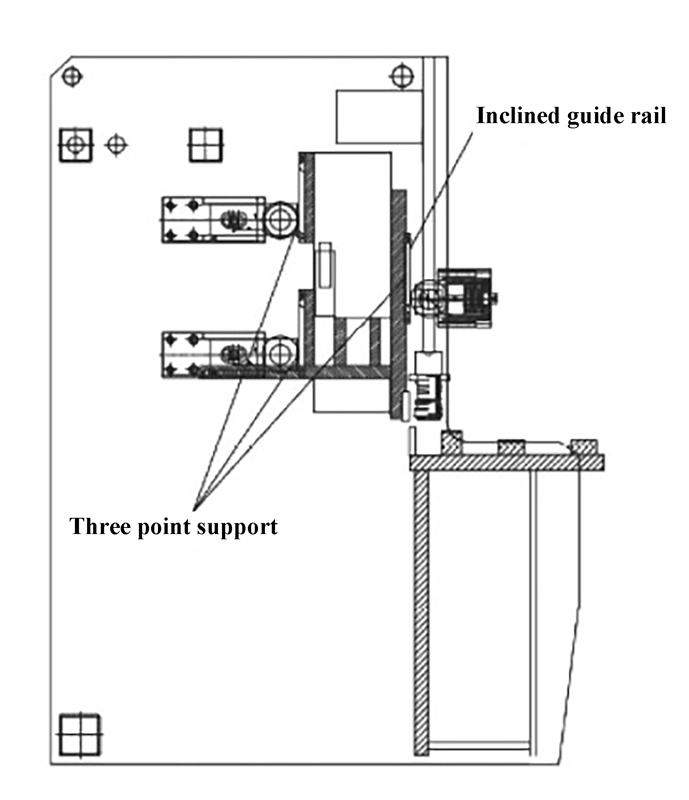
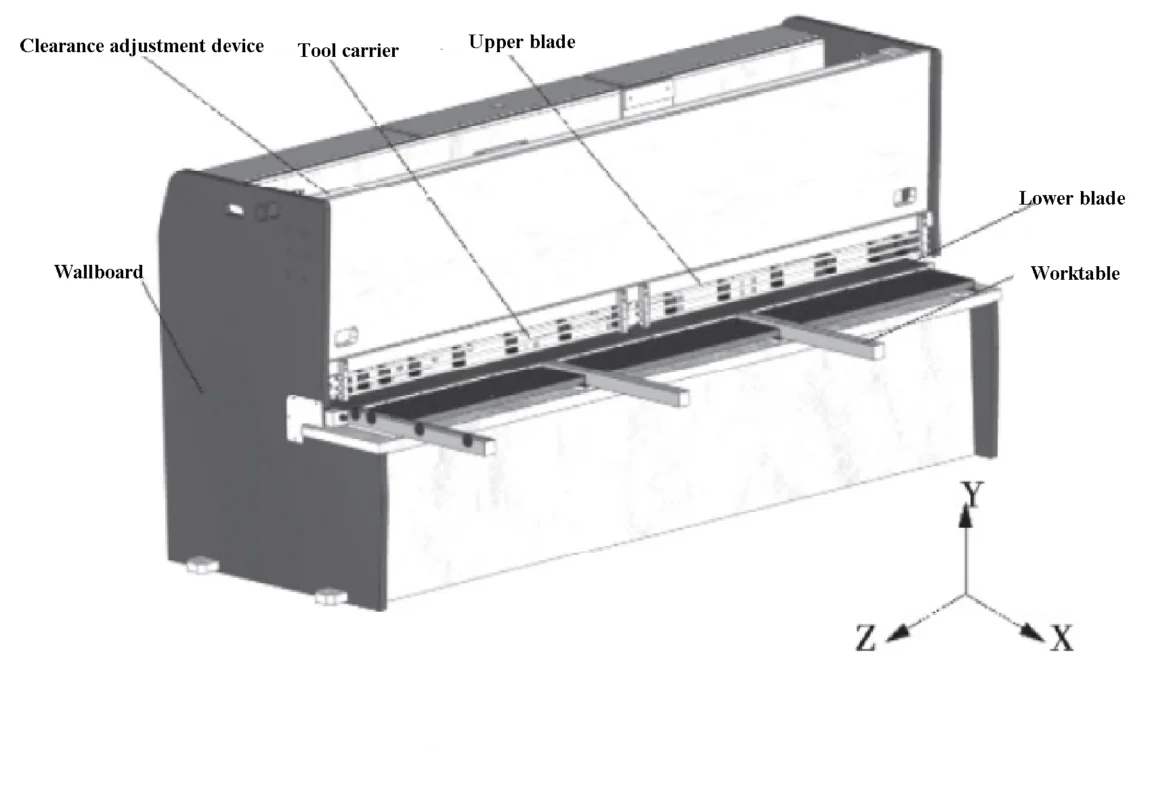
La figure 1 montre un modèle structurel d'une cisaille guillotine 6 x 3200 NC. Pendant le fonctionnement, le dispositif anti-retour, entraîné par la vis à rouleaux, ajuste la longueur de coupe. Le cylindre de pressage est ensuite comprimé par la plaque de cisaillement.
Une fois les paramètres de coupe, tels que le jeu de la lame et l'angle de cisaillement, définis, les vérins hydrauliques aux deux extrémités entraînent les lames supérieure et inférieure pour se déplacer et terminer le processus de coupe de la plaque.
Dans l'analyse de simulation, le congé de transition et le trou fileté sont ignorés et un modèle tridimensionnel simplifié est importé dans un logiciel d'analyse par éléments finis. Les deux côtés du support d'outil supérieur sont fixés avec des contraintes et un contact de liaison est établi pour simuler le soudage et la fixation du filetage des pièces du support d'outil supérieur.
Selon la formule de Norsali :
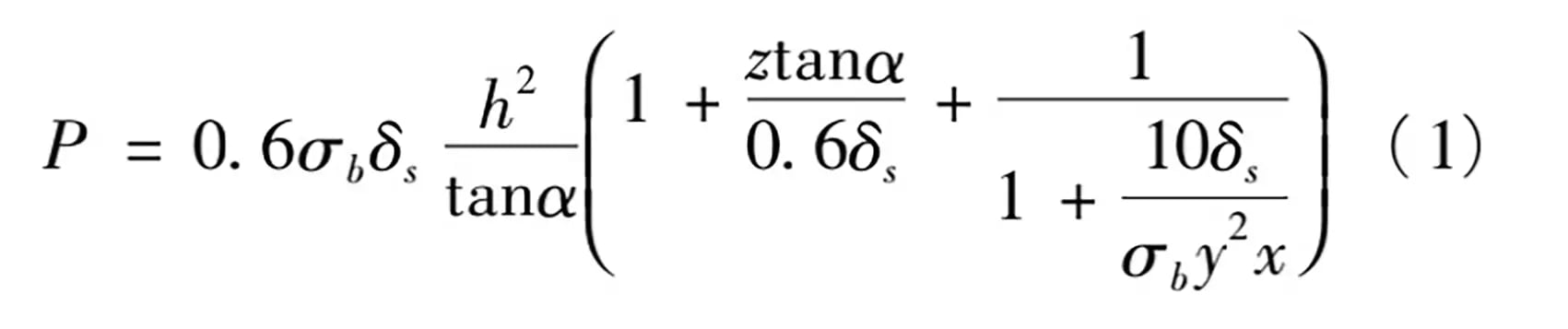
Dans la formule :
σb – Limite de résistance de la plaque à couper ;
δs – Ductilité de la tôle à découper ;
h – Épaisseur de la tôle à découper ;
α – Angle de cisaillement;
x, y, z – Le coefficient de force de flexion, la valeur relative du jeu latéral du tranchant et le coefficient de pressage.
La force de cisaillement verticale (P1) est calculée à 212,8 kN à l'aide de la formule (1), tandis que la force de cisaillement horizontale (P2) est estimée à 30% de la force de cisaillement verticale, soit 63,8 kN. Les forces de cisaillement verticales et horizontales sont appliquées à la tourelle supérieure et résolues à l'aide d'ANSYS Workbench.
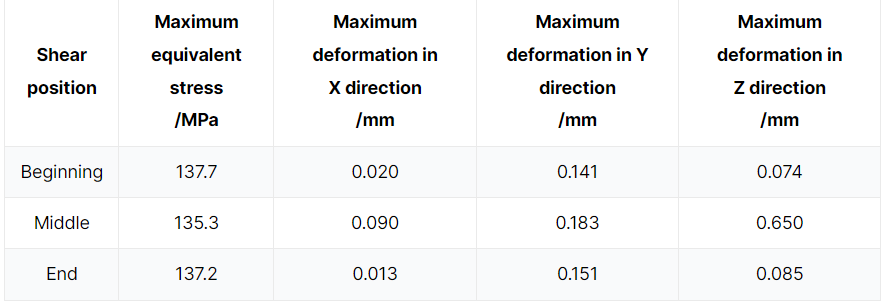
La déformation dans chaque direction au début, au milieu et à la fin du cisaillement est comparée et analysée. Comme le montre le tableau 1, la déformation du chariot supérieur dans la direction Y est la plus importante, et la déformation dans les directions X et Z peut être considérée comme négligeable en comparaison.
Les positions de départ et de fin de la déformation dans la direction Y sont approximativement égales et bien inférieures à la position médiane. Pendant le processus de cisaillement, la déformation du porte-outil supérieur présente une tendance concave.
Tableau 1 Contrainte équivalente maximale et déformation maximale dans les directions X, Y et Z du porte-outil supérieur
Les figures 2 et 3 montrent respectivement la contrainte équivalente maximale au milieu et la déformation maximale dans la direction Y.
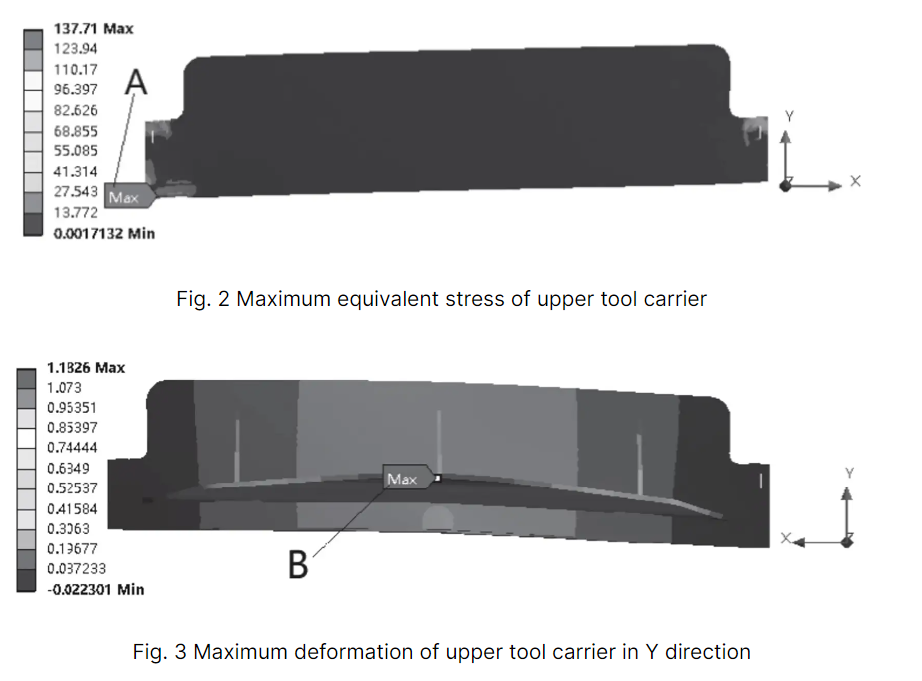
En analysant le tableau 1 et les figures 2 et 3, on peut déterminer que la contrainte équivalente du porte-outil supérieur est la plus élevée au début du processus de cisaillement. Cette contrainte est située au niveau de la position du vérin hydraulique et a une valeur de 137,7 MPa, ce qui est inférieur à la limite d'élasticité de 235 MPa pour le porte-outil supérieur.
Au milieu du processus de cisaillement, la déformation maximale du porte-outil supérieur dans la direction Y est observée au niveau de la plaque de support arrière B, avec une taille de 1,183 mm. Pendant ce temps, la déformation de la lame dans la direction Y est de 0,346 mm, ce qui est inférieur à 1 mm et répond aux exigences nécessaires.
Analyse dynamique transitoire
Dans la simulation dynamique, un curseur est placé à la position initiale de la lame supérieure et est constamment soumis à la force de cisaillement à une vitesse spécifiée. Le mouvement du curseur est utilisé pour simuler le processus de cisaillement de la plaque.
Comme le curseur ne transmet que la force de cisaillement, il a été réglé de manière à avoir un contact sans frottement avec la lame supérieure. Lors de la découpe de la tôle, le contact entre la lame supérieure et la tôle à découper est illustré à la figure 4. La longueur de contact (s) est de 8:1.
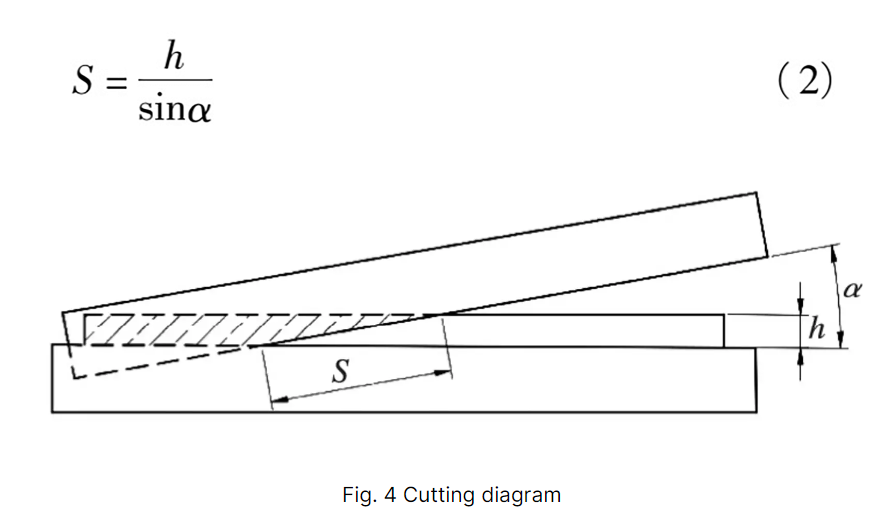
Pour simplifier le calcul, on suppose que la force de cisaillement est répartie uniformément sur une surface rectangulaire de longueur (s) et de largeur (t) de la lame. Par conséquent, le curseur est modélisé comme un cuboïde de même longueur (s) et de même largeur (t), comme illustré dans la figure 5.
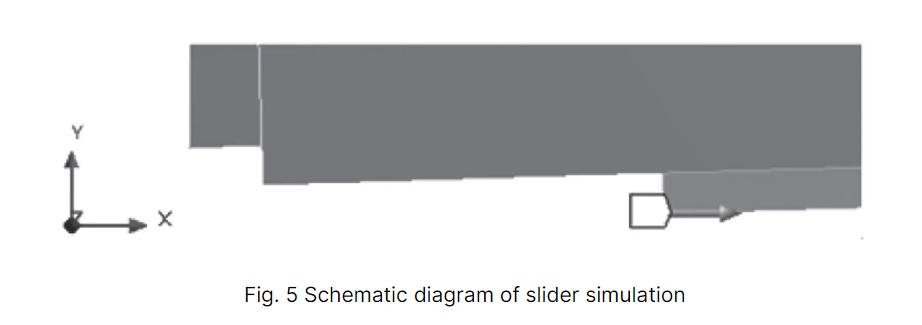
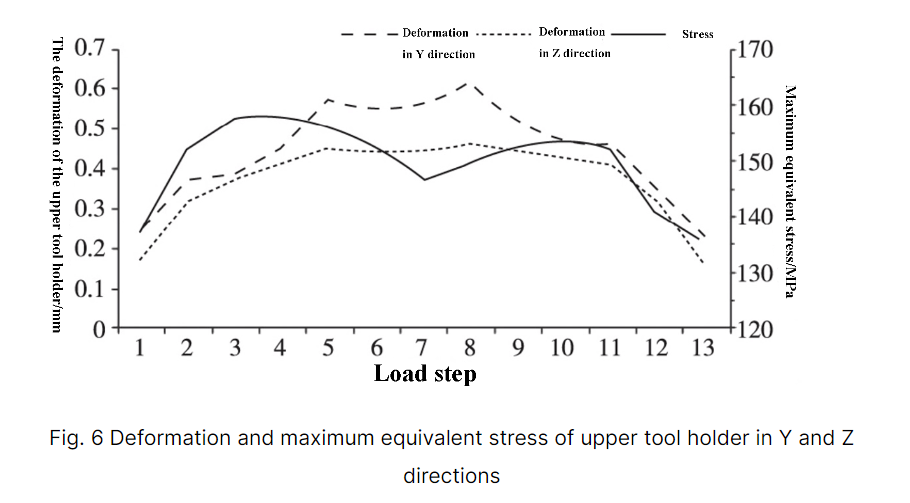
En résolvant la contrainte équivalente maximale et la déformation maximale dans les directions Y et Z à chaque position, les résultats sont présentés dans le tableau 2. La tendance de la déformation et de la contrainte du porte-outil supérieur pendant le processus de cisaillement est illustrée à la figure 6.
Tableau 2 Contrainte équivalente maximale et déformation maximale dans les directions Y et Z du porte-outil supérieur sous chaque niveau de charge
| Étape de chargement | Contrainte équivalente maximale | Déformation maximale dans la direction Y | Déformation maximale dans la direction Z |
| /MPa | /mm | /mm | |
| 1 | 138.1 | 0.265 | 0.181 |
| 2 | 153.2 | 0.38 | 0.33 |
| 3 | 158.4 | 0.403 | 0.386 |
| 4 | 159.2 | 0.469 | 0.426 |
| 5 | 157.5 | 0.592 | 0.463 |
| 6 | 153.8 | 0.571 | 0.454 |
| 7 | 148.1 | 0.58 | 0.461 |
| 8 | 150.3 | 0.635 | 0.478 |
| 9 | 153.7 | 0.543 | 0.458 |
| 10 | 154.9 | 0.477 | 0.446 |
| 11 | 153.2 | 0.482 | 0.425 |
| 12 | 141.8 | 0.358 | 0.336 |
| 13 | 136.4 | 0.25 | 0.175 |
Comme le montrent le tableau 2 et la figure 6, la déformation du porte-outil supérieur change avec le changement de la position de cisaillement. La déformation est importante au milieu et relativement faible et symétrique des deux côtés, ce qui correspond aux résultats de la simulation statique.
La déformation maximale du porte-outil supérieur dans les directions Y et Z se produit dans l'étape de charge 8, avec des valeurs de 0,635 mm et 0,478 mm, respectivement, qui sont inférieures à 1 mm.
La contrainte équivalente maximale se trouve dans l'étape de charge 4 et a une valeur de 159,2 MPa, ce qui est inférieur à la limite d'élasticité de 235 MPa pour le porte-outil supérieur.
Les figures 7, 8 et 9 affichent respectivement la déformation maximale et la contrainte équivalente maximale dans les directions Y et Z.
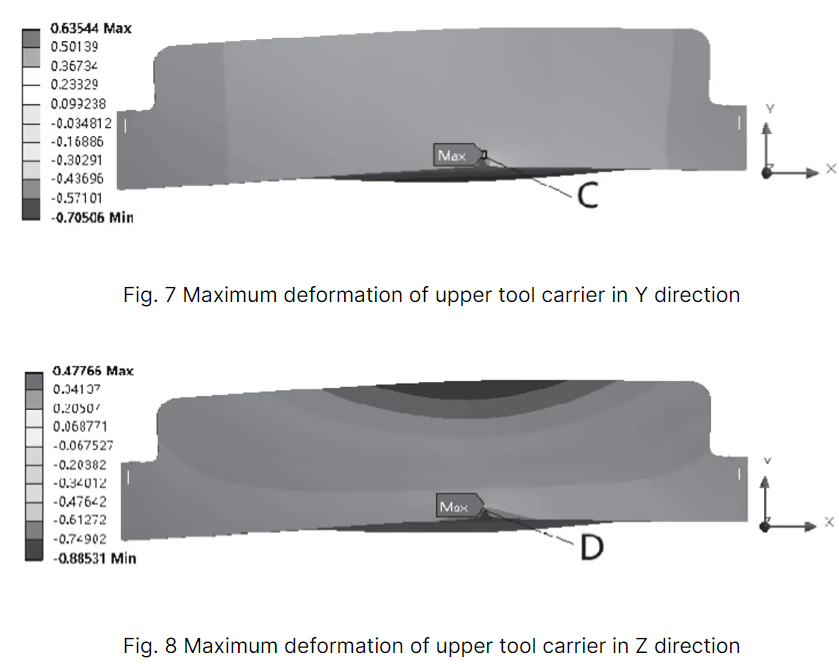

D'après les figures 7, 8 et 9, on peut observer que la déformation maximale du chariot supérieur dans la direction Y se produit au niveau de la lame C, tandis que la déformation maximale dans la direction Z se produit au niveau de la lame D. Les deux déformations sont inférieures à 1 mm, ce qui répond aux exigences de conception.
La contrainte équivalente maximale se produit à la position E du porte-outil supérieur sous l'effet du vérin hydraulique. La contrainte sur la lame est minimale et présente une bonne rigidité.
Analyse modale du cadre
Dans l'analyse modale, les quatre bases du cadre sont fixées et maintenues en place par des contraintes. La méthode Block Lanczos est sélectionnée comme méthode d'extraction de mode et le nombre de modes étendus est fixé à 4 pour résoudre les quatre premières fréquences naturelles de la structure du cadre.
Les quatre modes de vibration sont présentés dans la figure 10, et le tableau 3 présente les fréquences naturelles, les amplitudes et les formes modales des quatre modes structurels de vibration.
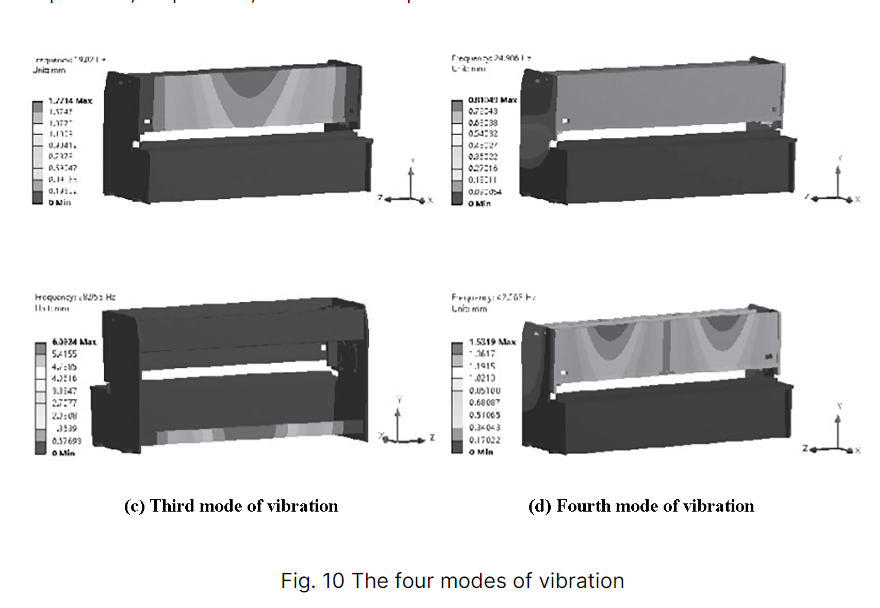
| Commande | Fréquence | Amplitudes | Mode de vibration |
| /Hz | /mm | ||
| 1 | 19.02 | 1.77 | Le panneau avant est plié vers l'avant dans la direction X |
| 2 | 24.98 | 0.81 | La partie supérieure du cadre se plie et pivote dans la direction Z |
| 3 | 28.96 | 6.09 | La poutre de support inférieure est courbée vers l'avant selon la direction X |
| 4 | 42.66 | 1.53 | Le panneau avant est plié d'avant en arrière dans la direction X |
D'après la figure 10 et le tableau 3, on peut constater que la déformation due aux vibrations du cadre affecte principalement le panneau avant et la poutre de support inférieure, provoquant des vibrations et un bruit importants. Lorsque la fréquence est de 19,02 Hz, l'amplitude du panneau avant est plus élevée, ce qui peut avoir un impact négatif sur le processus de cisaillement et diminuer sa précision.
Cependant, la fréquence de cisaillement de la cisaille à guillotine NC est de 9 fois par minute, ce qui est nettement inférieur à la fréquence naturelle du premier ordre et répond aux exigences d'un fonctionnement normal.
Il est important de minimiser l’influence des sources de vibrations externes pendant le processus de travail pour éviter une déformation excessive due aux vibrations.
Conception d'optimisation
L'analyse des caractéristiques statiques et dynamiques du processus de cisaillement révèle que la déformation de la tourelle supérieure présente une tendance concave pendant le cisaillement, ce qui peut avoir un impact sur la bavure et la précision dimensionnelle du découpage et réduire la qualité globale du cisaillement.
Pour améliorer la qualité de coupe, le jeu de la lame dans les paramètres de coupe peut être ajusté pour augmenter la rigidité de positionnement du porte-outil supérieur. Dans cet article, un dispositif de réglage du jeu de lame de type guide de biseau dynamique a été conçu, comme illustré à la figure 11.